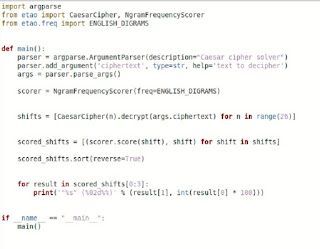
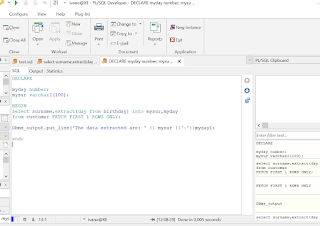
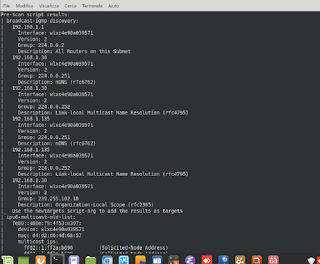
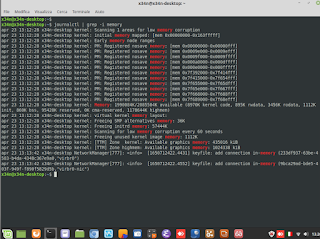
Encryption. Fermat's factorization and the quantum threat. Most of the most popular cryptographic systems are based on the fact that breaking keys requires the solution of an extremely complex mathematical problem, in which Fermat's Theorem on the factorization of prime numbers is used. The security of cryptographic systems, for the most part, lies in the fact that prime factorization is very complex. In practice, given a number with many digits, it is very difficult to determine its decomposition into these factors. However, in recent years, with the advent of quantum computers, we know that thanks to their remarkable computing capabilities, a cryptographic system could be breached in a relatively discrete time. Quantum computers work with complexity criteria divided into two Complexity Classes: P and NP. Class P provides that for a dimension 'N', there is a polynomial solution of 'N raised to P'. The NP class provides for a verification